Karekök bulma

"Not: Bilgisayarınızda Kök İşaretini Kullanmak İçin Alt+251 Tuş Kombinasyonunu Kullanabilirsiniz veya √ Bunu kopyalabilirsiniz"

Matematikte negatif olmayan bir gerçel $x$ sayısının temel karekök bulma işlemi $sqrt x$ şeklinde gösterilir ve karesi (bir sayının kendisiyle çarpılmasının sonucu) $x$ olan negatif olmayan bir gerçel sayıyı ifade eder.

Örneğin, 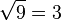$sqrt 9 = 3$ 'tür çünkü 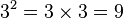$3^2 = 3times3 = 9$ 'dur.

Bu örneğin de ileri sürdüğü gibi karekök bulma, ikinci dereceden denklemlerin (genel olarak 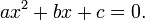$ax^2+bx+c=0. ,$ tipi denklemler) çözümünde kullanılabilir.

Karekök almanın sounucunda iki çözüm vardır. Negatif olmayan sayılar için bunlar temel kare kök ve negatif kare köktür. Negatif sayıların kare köklerini tanımlamak için ise sanal sayı ve karmaşık sayılar kavramları geliştirilmiştir.

Pozitif tam sayıların kare kökleri genel olarak irrasyonel sayılardır (iki tam sayının kesiri olarak ifade edilemeyen sayılardır).

Örneğin 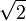$sqrt 2$ , tam olarak m/n (m ve n tam sayı olacak şekilde) şeklinde yazılamaz. Buna karşın bu sayı kenarları 1 birim olan bir karenin köşegen uzunluğuna eşittir.

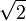$sqrt 2$ irrasyonel olduğunun bulunması Pythagoras'ın bir takipçisi olan Hippasus'a atfedilir. Bu konuyla ilgili şöyle bir rivayet anlatılır; Sayılara mutlak bir inançla bağlı olan Pisagor'un takipçilerinden birisi olan Metanpontumlu Hippasus, dik kenarları 1 birim olan bir dik üçgenin hipotenüs uzunluğunun rasyonel bir sayı olmadığını kanıtlamış. Bunu kabullenemeyen Pisagor, Hippasus'un kanıtlarının aksini de gösteremeyince, açık denizde Hippasus'u bir tekneden suya attırmış.

Kare kök sembolü ( $sqrt{ }$ ) ilk olarak 16. yüz yılda kullanılmaya başlandı. Latince kök demek olan radix kelimesinin baş harfinden, yani küçük r harfinden türetildiği söylenir. Ayrıca karekökte kök üç ile kök üçün çarpımı üçe eşittir. 1'den 10'a kadar olan doğal sayıların 2 kere yazıldıktan sonra (1010 veya 55) bu sayılar tekse karekökleri de tek sayı olur bu sayılar çift ise karekökleri de çift bir sayıdır.

Karekök Ortalama (matematikte ingilizcesinden dolayı ('root mean square', kısaltması RMS ya da rms) olarak da kullanılır), ayrıca kuadratik ortalama olarak da bilinir. Değişen miktarların büyüklüğünün ölçülmesinde kullanılan istatistiki bir ölçüttür. Değişimin artı ve eksi yönde olduğu dalgalarda özellikle çok faydalıdır.

Sürekli olarak değişen bir fonksiyonun sürekli olmayan değer serisi için hesaplanabilir. Karekök ortalama ismi karelerin ortalamasının karekökünün alınmasından gelir.

ö(((((Ö)))))<#redirect[[[[Kategori:#redirect[[]]]]]]== Tanım ==

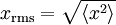$x_text{rms} = sqrt{ langle x^2 rangle} ,!$ ( $langle ldots rangle$ ) ben

Karekök ortalama hesaplanması

$n$ sayıdaki değerlerin 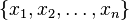${x_1,x_2,dots,x_n}$ yusuf;

$x_{mathrm{rms}} = sqrt {{1 over n} sum_{i=1}^{n} x_i^2} = sqrt {{x_1^2 + x_2^2 + cdots + x_n^2} over n}$

olarak hesaplanır.

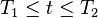$T_1 le t le T_2$ aralığında sürekli bir f(t) fonksiyonu için karşılık gelen formülü;

$f_{mathrm{rms}} = sqrt {{1 over {T_2-T_1}} {int_{T_1}^{T_2} {[f(t)]}^2, dt}}$

Kullanım yerleri

Bir fonksiyonun RMS değeri çoğunlukla fizik ve elektrik mühendisliğinde kullanılır. Örneğin, $R$ direncindeki bir iletken tarafından harcanan $P$ gücünü hesaplamak isteyebiliriz. İletkenden sabit bir $I$ akımı aktığında bu hesabı yapmak kolaydır. Basitçe:

$P = I^2 R,!$

Ancak akım değişen bir $I (t)$ fonksiyonu ise burada rms değeri devreye girer.

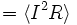$P_mathrm{avg},!$	$= langle I^2R rangle ,!$ ( $langle ldots rangle$ aritmetik ortalamayı ifade eder)
	$= Rlangle I^2 rangle,!$ (R bir sabit olduğuna göre ortalamanın dışına çıkarılabilir)
	$= I_mathrm{rms}^2R,!$ (RMS in tanımından)

Aynı metod ile;

$P_mathrm{avg} = {V_mathrm{rms}^2over R},!$

$P_mathrm{avg} = V_mathrm{rms}I_mathrm{rms},!$

Ancak bu tanım gerilimın ve akımın birbiriyle orantılı olduğu (yani yükün resistif olduğu) varsayımı temel alınarak yapılmıştır ve genellenemez.

Şebeke güçlerinde olduğu gibi alternatif akımın genel durumunda, $I (t)$ sinusoidal akım olduğunda rms değeri yukarıdaki sürekli durum denkleminden kolaylıkla hesaplanabilir. $I p$ yi tepe genliği olarak tanımladığımızda:

$I_{mathrm{rms}} = sqrt {{1 over {T_2-T_1}} {int_{T_1}^{T_2} {(I_mathrm{p}sin(omega t)}, })^2 dt},!$

$I p$ positif bir gerçek sayı olduğuna göre,

$I_{mathrm{rms}} = I_mathrm{p}sqrt {{1 over {T_2-T_1}} {int_{T_1}^{T_2} {sin^2(omega t)}, dt}}$

Trigonometrik fonksiyonun karesinin alınmasını elimine etmek için trigonometrik bir varlık kullanıldığında:

$I_{mathrm{rms}} = I_mathrm{p}sqrt {{1 over {T_2-T_1}} {int_{T_1}^{T_2} {{1 - cos(2omega t) over 2}}, dt}}$

$I_{mathrm{rms}} = I_mathrm{p}sqrt {{1 over {T_2-T_1}} left [ {{t over 2} -{ sin(2omega t) over 4omega}} right ]_{T_1}^{T_2} }$

Fakat aralık tam periyotlardan oluşan bir tam sayı olduğu için (rms in periyodik fonksiyonlar için tanımından $omega = frac{2 pi}{t}$ ) Sinüs değerler iptal edilir.

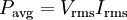
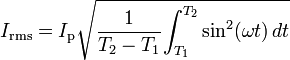
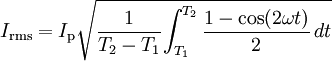
$I_{mathrm{rms}} = I_mathrm{p}sqrt {{1 over {T_2-T_1}} left [ {{t over 2}} right ]_{T_1}^{T_2} } = I_mathrm{p}sqrt {{1 over {T_2-T_1}} {{{T_2-T_1} over 2}} } = {I_mathrm{p} over {sqrt 2}}$

Saf bir sinüs dalgası için; tepe voltajı = RMS voltajı x 1.414( $sqrt{2}$ ) tür. Tepeden tepeye voltajı bunun iki katıdır.